A Level H2 Math Tuition
(Improve 2 Grades Or More)
(Improve 2 Grades Or More)
Worried about not doing well in H2 Math?
H2 Math Tuition, is it needed? In Odyssey Math, in addition to focusing on students’ mathematical concepts and the difficulties they faced understanding mathematics, Mr Tan will always try his best to motivate his students and at the same time identify weaknesses and gaps in his students’ mathematical understanding. The key to teaching is not only to just go through mathematics during the 2 hours class but also to be genuine in helping students during and even after lessons. Mr Tan seeks to work with his students and provide them the necessary support as much as possible. For H2 Math, the key to doing well is to apply the right concepts and do enough practice questions to hone their math foundation.
$240/ 4 weeks (Sec)
$280/ 4 weeks (JC)
Affordable, no hidden charges, no registration and administrative fees.
Free Trial Available
First lesson is a free trial! No obligations to continue!
Premium Resources
Math resources for all the math help you need
Math tuition that provides FREE e-learning
for enrolled students
1) Secondary 3,4,5 Additional Mathematics (monthly access)
2) Secondary 3,4,5 Additional Mathematics (yearly access)
3) Secondary 3,4,5 Elementary Mathematics (monthly access)
4) Secondary 3,4,5 Elementary Mathematics (yearly access)
5) Free A/E Math Mini Course (Login to Enroll For Free)
6) H2 Mathematics (yearly access)
7) Secondary 1 Mathematics (yearly access)
8) Secondary 2 Mathematics (yearly access)
9) Lesson Recordings For Mathematics
A) Sec 1 Math Question Bank
B) Sec 2 Math Question Bank
C) Sec 3 A Math Question Bank
D) Sec 3 E Math Question Bank
E) Sec 4 A Math Question Bank
F) Sec 4 E Math Question Bank
G) H2 Math Question Bank (Pure Math)
H) H2 Math Question Bank (Pure Math + Statistics)
Why Odyssey Math?
Results Oriented
Why send your child in the first place if it doesn’t solve his or her problem? We assure that if our students follow our guidance , do the assignments given and at the same time ask questions we can assure that they will improve their grades in H2 Mathematics. We are always there for the students when they need it and this is exactly what they need to improve their results. Mr Tan seeks to instill confidence in students, give them encouragement and motivation and at the same time be very genuine towards the development of the students both academically and holistically. Students who put in the hard work, follow his guidance and make use of his resources will be able to improve in mathematics.
Experienced and Qualified Math Tutor
With 11 years of coaching mathematics and having a passion for mathematics, Mr Tan has graduated with a math degree with distinction from NUS and continues to impart knowledge to his students. Throughout his time studying and coaching mathematics, he has gain a strong understanding of the subject. As such, Mr Tan is able to teach H2 Math in a simplified manner and generous in providing tips and tricks to tackle the subject. This will allow students to better understand the subject and give them an edge over the rest.
Affordable H2 Math Tuition with maximum value
You can be assured that students will benefit from our H2 Math Tuition at an affordable rate. Our aim is to help the students but at the same time provide the maximum values to students and reducing the cost burden to many parents.
24/7 Support
We stay committed to answering students’ queries even after lesson hours. Mr Tan believes that when it comes to education services, learning does not end after lesson hours.
Small Class Sizes
In Odyssey Math, we aim to provide equal attention to all of us students. As such, we keep the class size small (6 to 8 students).
Testimonials of our teaching
Don’t just listen to what we have to say, see below on the testimonials from our students.
Our H2 Math Tuition Structure
Our H2 Math Tuition structure is broken down into 4 phases below. Students will gain conceptual understanding of topics, thereafter practice in class and will be assigned homework to be reviewed in subsequent lessons. Topical tests will be given to test their aptitude in the topics learnt after which we will review with them and resolve misconceptions and weaknesses in concepts.
Introduction of Topics
Practice and Homework
Topical Test
Review
H2 Math Topics Covered
- Concepts of function, domain and range
- Usage of notations
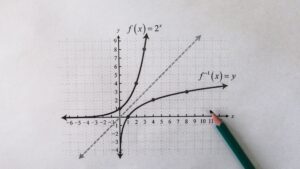
- Inverse functions
- Composite functions
- Conditions for the existence of inverse and composite functions
- Domain restriction to obtain an inverse function
- Relationship between a function and its inverse
- Use of a graphing calculator to graph a given function
- Important characteristics of graphs such as symmetry, intersections with the axes, turning points and asymptotes
- Determining equations of asymptotes, axes of symmetry, and restrictions on the possible values of x and/or y
- Effect of transformations on the graph of y=f(x) and combinations of various transformations
- Parametric equations and their graphs
- Formulating an equation, a system of linear equations or inequalities based on a problem
- Using graphing calculator to solve an equation
- Using a graphing calculator to solve a system of linear equations
- Solving inequalities where the numerator and denominator are either linear or quadratic expressions that are either factorisable or always positive
- Concept of absolute value of x and use of relations
- Using graphical methods to solve inequalities
- Understanding sequence and series for finite and infinite cases
- Sequence as function
- Using the summation notation
- Sum and difference of two series
- Summation of series by the method of differences
- Convergence of a series and the sum to infinity
- Formula for the nth term and the sum of a finite arithmetic series
- Formula for the nth term and the sum of a finite geometric series
- Condition for convergence of an infinite geometric series
- Formula for the sum to infinity of a convergent geometric series
- Vectors in three dimensions
- Addition, subtraction and multiplication of a vector by a scalar and their geometrical interpretations
- Use of notations in vectors
- Position, displacement and direction vectors
- Magnitude of a vector
- Unit vectors
- Distance between two points
- Collinearity
- Use of the ratio theorem in geometrical applications
- Scalar product of vectors
- Vector product of vectors
- Angle between two vectors
- Vector and cartesian equations of lines and planes
- Finding the foot of the perpendicular and distance from a point to a line or to a plane
- Finding the angle between two lines, between a line and a plane, or between two planes
- Relationships between two lines (either coplanar or skew)
- Relationships between a line and a plane
- Relationships between two planes
- Extension of the number system from real numbers to complex numbers
- Complex roots of quadratic equations
- Conjugate of a complex number
- Four operations of complex numbers
- Equality of complex numbers
- Conjugate roots of a polynomial equation with real coefficients
- Representation of complex numbers in the Argand diagram
- Calculation of modulus and argument of a complex number
- Multiplication and division of two complex numbers expressed in polar form
- Graphical integration of various derivative functions
- Relating the graph of y=f'(x) to the graph of y=f(x)
- Implicit differentiation
- Determining the nature of the stationary points
- Locating maximum and minimum points using a graphing calculator
- Finding the approximate value of a derivative at a given point using a graphing calculator
- Finding equations of tangents and normals to curves, including cases where the curve is defined implicitly or parametrically
- local maxima and minima problems
- connected rates of change problems
- Standard series expansion
- Derivation of first few terms of the Maclaurin series by repeated differentiation, repeated implicit differentiation or using standard series
- Know the range of values of x for which a standard series converges
- Understanding the concept of approximation
- Small angle approximations
- Integration of new forms of algebraic and trigonometric expressions
- Integration by a given substitution
- Integration by parts
- Understanding definite integral as a limit of sum
- Definite Integral as the area under a curve
- Evaluating definite integrals
- Find the area of a region bounded by a curve and lines parallel to the coordinate axes, between a curve and a line, or between two curves
- Area below the x-axis
- Finding the area under a curve defined parametrically
- Finding the volume of revolution about the x- or y-axis
- Finding the approximate value of a definite integral using a graphing calculator
- Solving general solutions and particular solutions of differential equations
- Formulating differential equation based on a problem situation
- Interpreting differential equation and its solution based on a problem situation
- Permutation and combination
- Arrangements of objects in a line or in a circle, including cases involving repetition and restriction
- Addition and multiplication of probabilities
- Mutually exclusive events and independent events
- Use of tables of outcomes, Venn diagrams, tree diagrams, and permutations and combinations techniques to calculate probabilities
- Calculation of conditional probabilities in simple cases
- Concept of discrete random variables, probability distributions, expectations and variances
- Concept of binomial distribution
- Usage of mean and variance of binomial distribution without proof
- Concept of normal distribution
- Standard normal distribution
- Symmetry of the normal curve and its properties
- Solving problems involving E(aX+b), E(aX+bY), Var(aX+b), Var(aX+bY), where X and Y are independent
- Concepts of population and simple random sample
- Concept of the sample mean as a random variable
- Distribution of sample means from a normal population
- Central Limit Theorem
- Calculation and use of unbiased estimates of the population mean and variance from a sample
- Null Hypothesis and Alternative Hypothesis
- Critical region, critical value, level of significance and p-value
- Formulating hypotheses
- 1-tail and 2-tail tests
- Interpretation of the results of a hypothesis test in the context of the problem
- Scatter diagram
- Correlation coefficient as a measure of fit of a linear model to scatter diagram
- Finding and interpreting the product moment correlation coefficient, particularly for values close to -1, 0 and 1
- Concepts of linear regression and method of least squares to find equation of the regression line
- Interpolation and extrapolation
- Use of the appropriate regression line to make prediction
- Use of a square, reciprocal or logarithmic transformation to achieve linearity
What Our Students Have to Say about Odyssey Math Tuition
Our Location
We are located near Eunos MRT Station.
Icon @ Changi B1-03, Singapore, 419741
Learn more about Odyssey Math
- Learn more about Singapore Math Specialist
- Learn more about Math Tuition Singapore
- Learn more about Sec 1 Math Tuition
- Learn more about Sec 2 Math Tuition
- Learn more about E Math Tuition
- Learn more about A Math Tuition
